A Turing Machine (TM) is a mathematical model which consists of an infinite length tape divided into cells on which input is given. It consists of a head which reads the input tape. A state register stores the state of the Turing machine. After reading an input symbol, it is replaced with another symbol, its internal state is changed, and it moves from one cell to the right or left. If the TM reaches the final state, the input string is accepted, otherwise rejected.
Turing machine was invented in 1936 by Alan Turing.
It is an accepting device which accepts
Recursive Enumerable Language generated by type 0 grammar.
1. It has an external memory which remembers arbitrary long sequence of input.
2. It has unlimited memory capability.
3. The model has a facility by which the input at left or right on the tape can be read easily.
4. The machine can produce a certain output based on its input.
The time complexity of a Turing machine is the number of tape movements when initiated for
certain input symbols. The space complexity is the number of tape cells written.
Time complexity: T(n) = O(n log n)
Space complexity: S(n) = O(n)
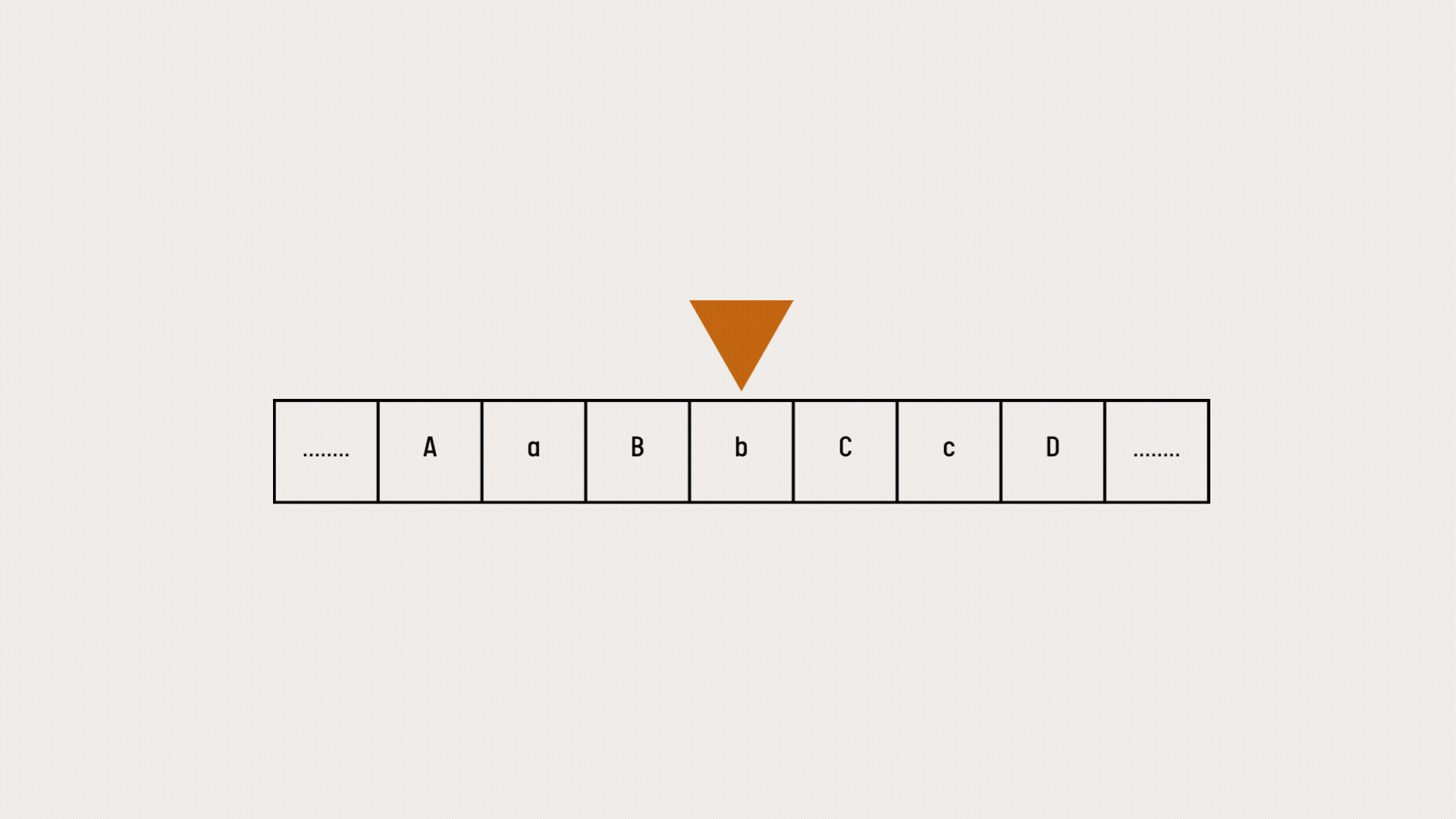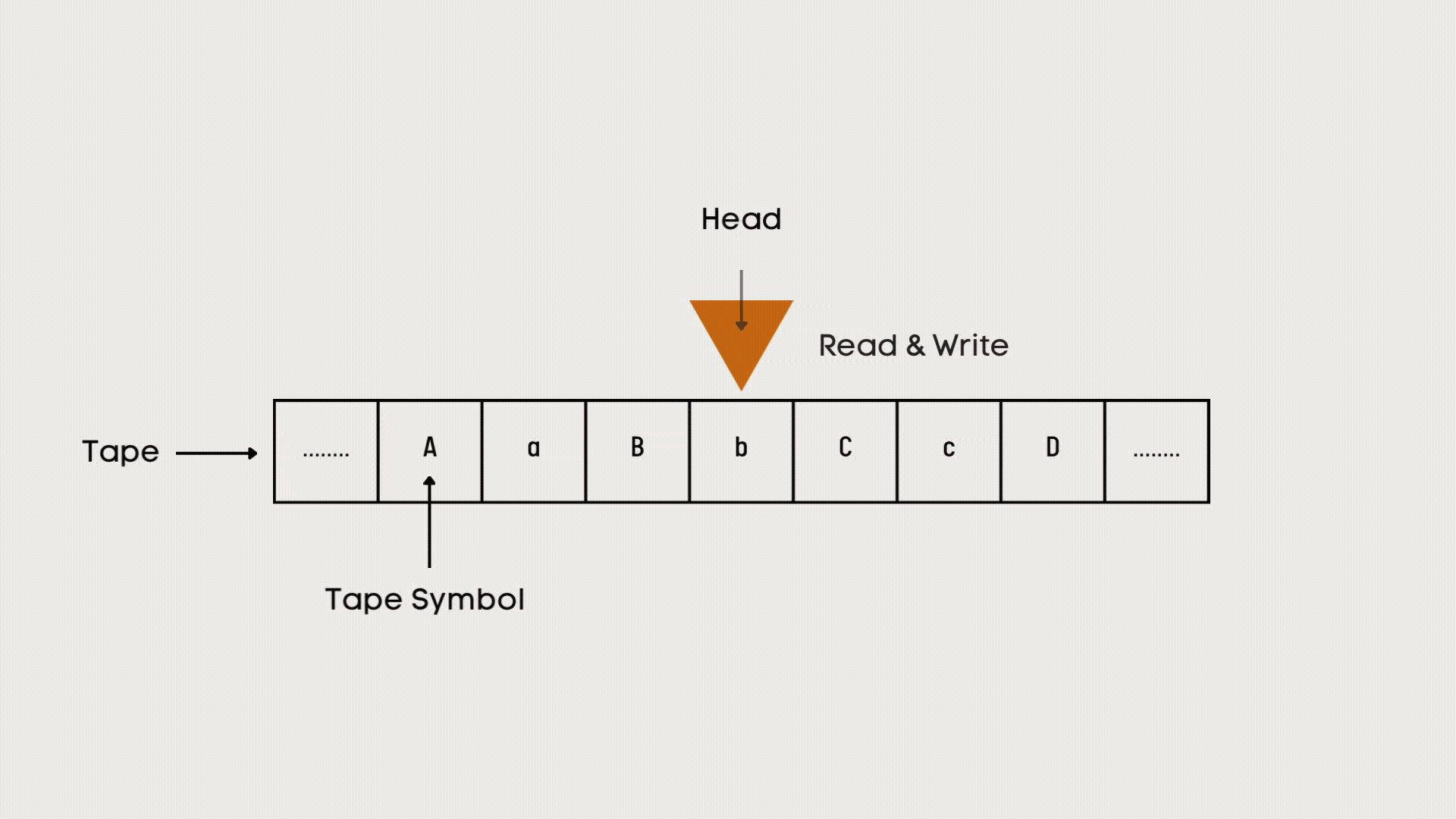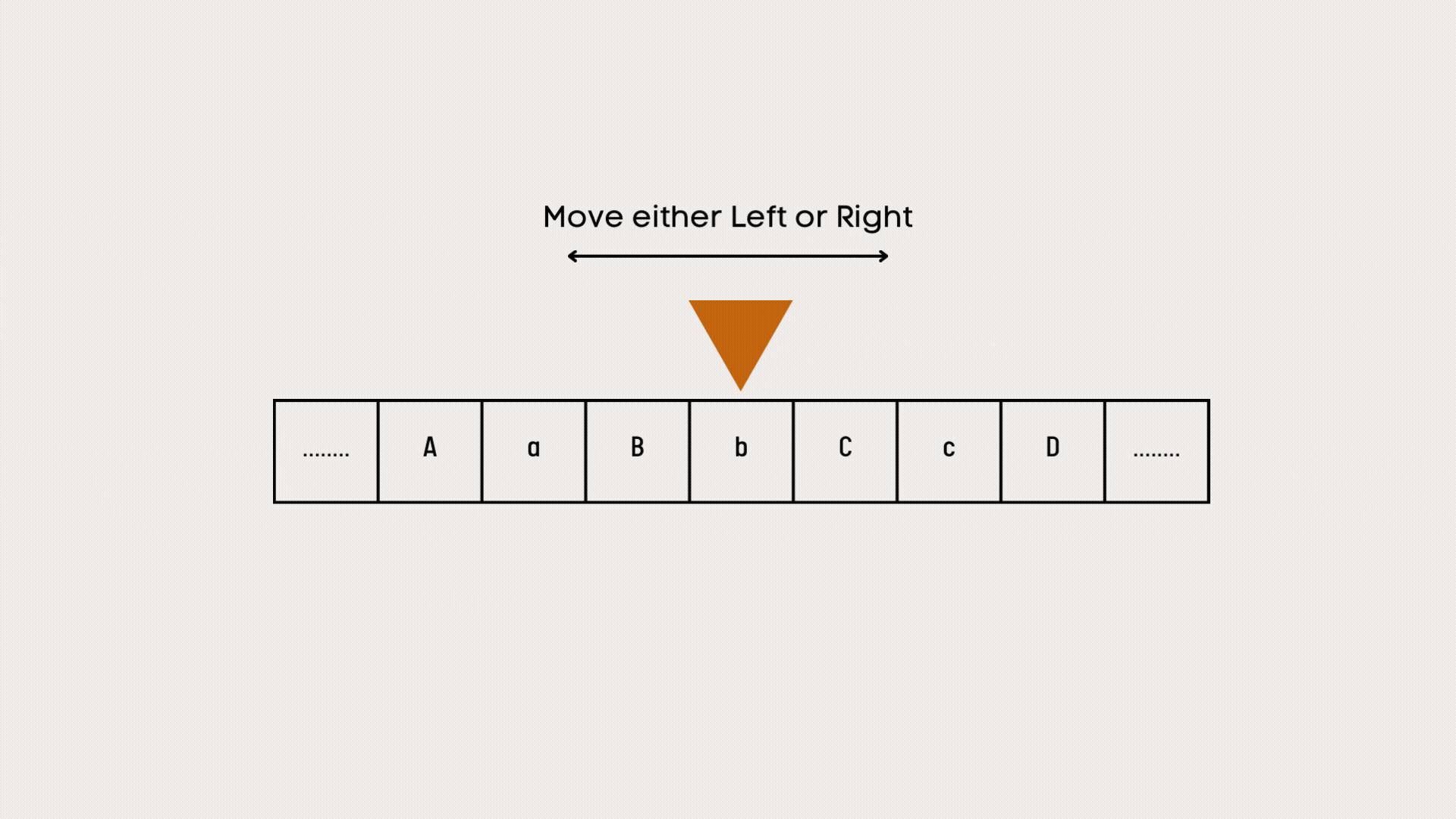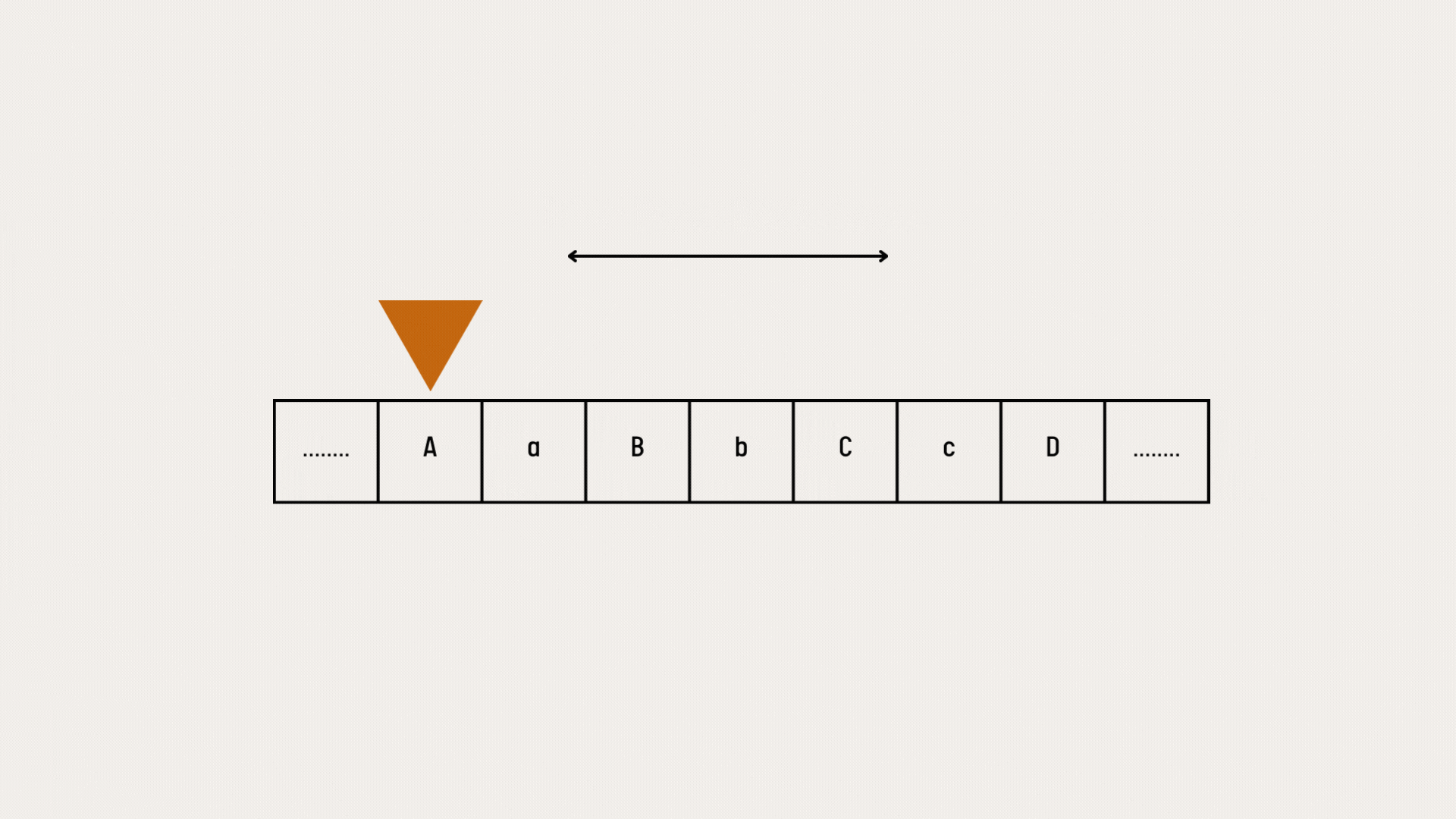
A tape on which data can be sequentially stored. The tape consists of fields, which are sequentially arranged. Each field can contain a character of a finite alphabet. This tape has no limits, it goes on infinitely in both directions. A Turing machine also contains a head moving in both directions over the tape. This head can read and write one character from the field over which the head resides. The Turing machine is at every moment in a certain state, one of a finite number of states. A Turing is a set of transitions that determines, for a given state and character, a new state, a character to write beneath the head, and a head movement direction. A finite table of instructions, which are generally quintuples, but occasionally quadruples.
A Turing Machine can be formally described as
a 7-
tuple (Q, X, ∑, δ, q0, B, F) where:
Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
δ is a transition function;
δ : Q × X → Q × X × {Left_shift, Right_shift}.
q0 is the initial state
B is the blank symbol
F is the set of final states
The machine positions its head over a cell and "reads" (scans) the symbol there. Then, as per the
symbol and its present place in a finite table of user-specified instructions, the machine:
1. Writes a symbol (e.g., a digit or a letter from a finite alphabet) in the cell (some models allowing
symbol erasure or no writing).
2. Then either moves the tape one cell left or right (some models allow no motion, some models
move the head).
3. Then either proceeds to a subsequent instruction or halts the computation (as determined by
the observed symbol and the machine's place in the table).